applebta.blogg.se - Z score table to standard normal distribution

Probability Density Function (P.D.F.) of a normal distribution Probability Density Function of Normal DistributionĪ Probability Density Function (PDF) for a Normal Distribution with a continuous random variable x, with mean μ, variance σ 2 and standard deviation σ is given as:

The area under the curve is equal to 1, i.e. ∫f(x)dx = 1 (x belongs to ∞, −∞).

The density function is always non-negative i.e. f(x) > 0, for all possible values of x.

Let us consider a continuous random variable x with density function f(x), then the Probability Density Function should satisfy the following conditions: In statistics theory, PDF is popularly known for helping us calculate the probabilities associated with the random variables. Probability Density Function determines the probability of a random variable to take a value bound between the given intervals. Probability Density Function (PDF) is a statistical function in probability theory whose value in the sample space at any given point or sample, can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. The tails of a normally distributed graph approach the x-axis but never quite really touch. In a normal distribution graph, the further a value is from the mean, the less likely it is to occur and the ones that cluster around the mean are more likely to occur.ĥ.

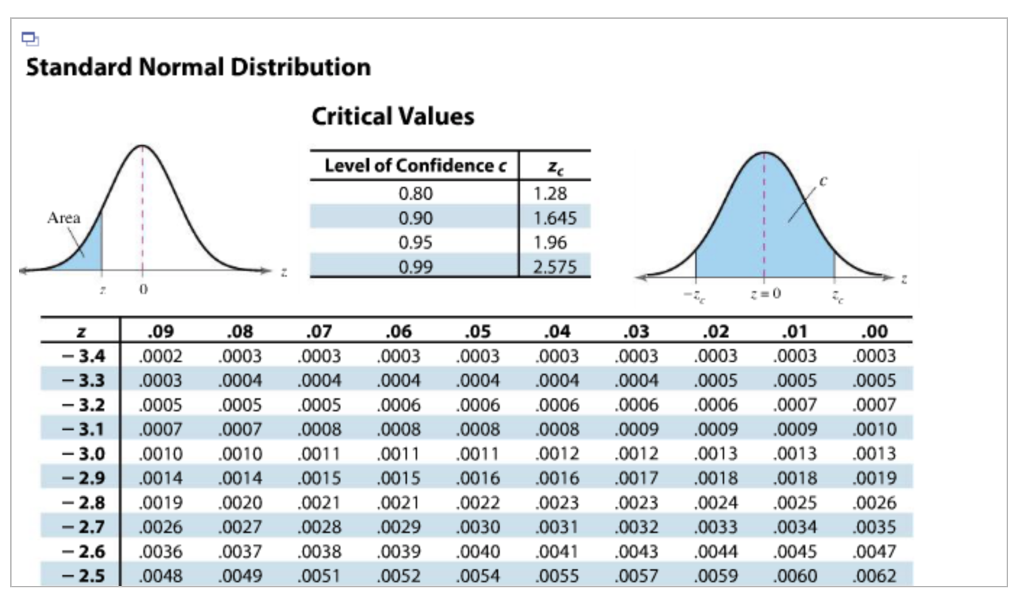
For a normal distribution the mean, median and mode are equalĤ. the values are evenly distributed to form identical halves on both sides of the mean.ģ. Normal distribution is symmetrical on both sides of the mean i.e. If the scores of these students were to be mapped on a graph, it would lend itself the shape of a bell curve.Įxample 2: Normal Distribution of Weights of Newborn BabiesĢ. A large number of students will score the average score (say 65 out of 100), while a few will score near 50s or 80s and fewer will fail the test or get a perfect score. Examples of Normal DistributionĮxample 1: Normal Distribution of Test ScoresĪ Normal Distribution can be observed by analyzing the test scores of students for any particular course. Normal distribution is one of the most common types of distribution patterns used in statistics and real life. This characteristic lends the normal distribution a bell curve like shape which is symmetric about the mean.

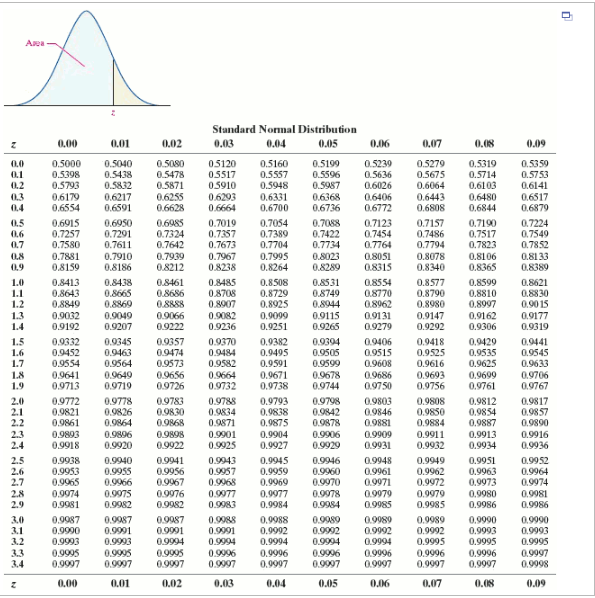
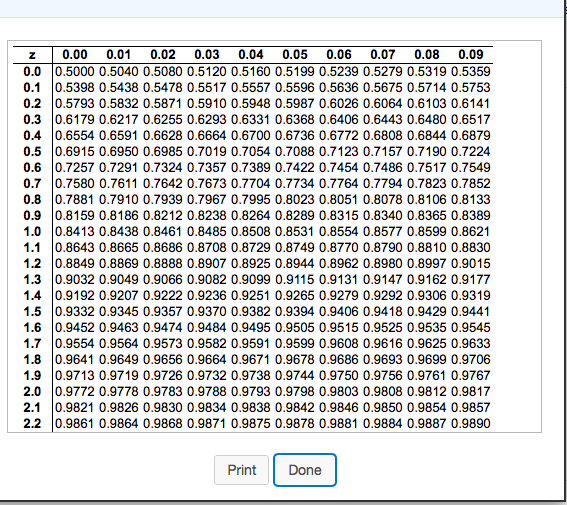
Normal Distribution also known as Gaussian Distribution (named after the German mathematician Carl Gauss who first described it) is a continuous probability distribution in which the occurrence of data is more clustered near the mean than the occurrence of data far from the mean.